Skip to content

parent link: 0011 Algorithms ♾️

graph 기초#

상태: 정리완료
태그: graph

그래프는 엔티티와 그들 사이의 연결관계를 표현한다. 정점의 집합과 이들을 연결하는 간선의 집합으로 표현이 가능하며, 여러가지 표현의 방법이 있다.

그래프의 종류#

  • 방향성이 없는 그래프 (무향 그래프) == 어디로든 갈 수 있다.
  • 방향성이 있는 그래프 (유향 그래프) == 반대로는 갈 수 없다.
  • 가중치 그래프 == 노드에서 노드로 간선을 따라 이동할 때 소요되는 비용
  • 사이클이 있는 그래프 == 한 노드에서 시작해 자기 자신으로 돌아올 수 있다면 사이클이 있다.
  • 사이클이 없는 그래프 == 모든 노드에 대하여 사이클이 존재하지 않는다면 사이클이 없다고 표현할 수 있다.
  • 완전 그래프 == 정점들에 대해 가능한 모든 간선을 가진 그래프
  • 부분 그래프 == 원래 그래프에서 일부 정점이나 간선을 제외한 그래프

용어정리#

  • 인접 (Adjacency) == 두 개의 정점에 간선이 존재하다.
  • 경로 == 간선을 순서대로 나열 OR 정점을 순서대로 나열
    • 단순경로 == 같은 정점이 경로 안에 두 번 출현하지 않는 경로 == 사이클이 없다는 뜻.
    • 사이클 == 시작한 정점에서 끝나는 경로

그래프 표현방법#

  • 인접행렬 : 모든 정점에 대한 이차원 행렬을 가지고 가중치가 없으면 불리언, 있으면 정수형으로 저장

    • 두 정점의 번호를 각각 행 번호, 열 번호에 할당. (n,m)에 인접해 있지 않다면 false 혹은 ♾️ 를 저장
    • 방향성이 없는 경우 대칭행렬이 될 수밖에 없다.
    • 정점의 번호들의 인덱스만 가지고 바로 알 수 있기 때문에 코드가 간결.
    • 불필요한 공간낭비가 발생할 수 있다는 단점.

    • 2차원 벡터로 구현

      매우 직관적으로 코딩할 수 있지만 벡터 특성상 오버헤드가 발생하고 동적으로 생성한 데이터가 파편화 되어 캐시 효율이 떨어진다는 단점 존재.

      std::vector< std::vector< int >> graph(n);
for (const auto& e : edges) {
    graph[e.first].emplace_back(e.second);
}

    Untitled(3).png

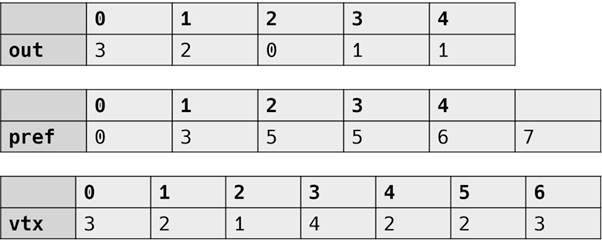
    • 1차원 벡터로 구현

      2차원 벡터의 모든 요소를 하나의 일차원 벡터(vertices)에 몰아넣었다. 어느 정점이 몇개의 인접노드를 갖고 있는지 파악하기 위해 out을 사용하고, 정점이 연결된 vertices 배열의 시작 인덱스를 알기 위해 prefix를 사용한다.

      [수정] outdegree는 리스트 생성 이후 전부 0으로 초기화 되는 것 같다. 따라서 각 정점과 연결된 노드의 개수를 알기 위해선 prefix[i+1] - prefix[i] 작업을 해야 한다. 사실 i번 정점의 인접 노드들 = [prefix[i], prefix[i+1]) 구간의 vertices만 알면 된다.

      std::vector< int > outdegree(n);
std::vector< int > prefix(n + 1);
std::vector< int > vertices(edges.size());
for (const auto& e : edges) {
    ++outdegree[e.first];
}
std::partial_sum(outdegree.begin(), outdegree.end(), std::next(prefix.begin()));
for (const auto& e : edges) {
    vertices[prefix[e.first] + --outdegree[e.first]] = e.second;
}

      Untitled(4).png

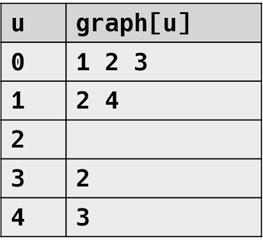
  • 인접리스트 : 정점마다 해당 정점으로부터 나가는 간선의 정보를 저장.

    • 간선의 개수가 적은 경우 유용. 모든 인덱스를 링크드 리스트형식으로 저장.

    • 한 정점에서 특정 정점으로 가야 할 때 하나씩 살펴봐야 한다는 단점.

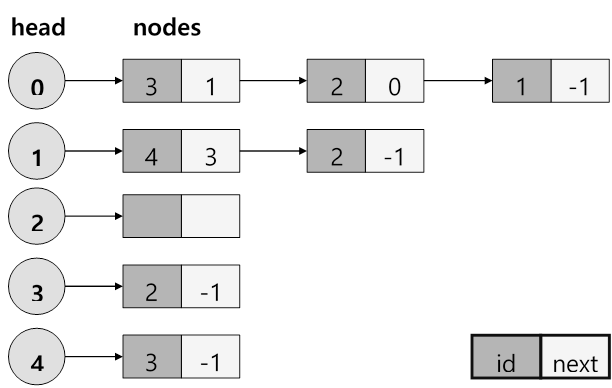
      Untitled.png

    • 배열을 사용한 인접리스트

      nodes의 next는 포인터를 가리키는게 아니라 배열의 인덱스를 가리킨다는 점에 유의하자. 사실 어떻게 보면 그게 그거긴 함. 결국 가리킨다는 본질은 그대로니까. head[] 각 인덱스는 인접노드의 nodes[] 배열에 대한 시작 인덱스를 가리킨다. 그렇게 계속 next, next 따라 이동하다 마지막 인접노드의 next 는 항상 -1로 끝난다.

      struct LinkedListNode {
    int id;
    int next;
};
std::vector< LinkedListNode > nodes(edges.size());
std::vector< int > head(n, -1);
for (int i = 0; i < static_cast< int >(edges.size()); ++i) {
    nodes[i].id = edges[i].second;
    nodes[i].next = head[edges[i].first];
    head[edges[i].first] = i;
}

      Untitled(1).png

      nodes

      Untitled(2).png

      head

  • 간선의 배열 : 간선을 배열에 연속적으로 저장한 방법

그래프 탐색#

  • DFS : 한 방향으로 갈 수 있는 곳을 우선으로 끝까지 탐색. 인접 정점이 더 없는 경우 이전에 지나쳤던 곳으로 돌아와 다른 방향의 정점으로 탐색을 계속 반복.

    • 재귀 or 스택
    • LIFO 가장 마지막에 넣은 자료가 가장 먼저 나온다.
    • top := -1 사실 단순한 스택이라면 굳이 스택까지 만들 필요조차 없다.
    • push(), pop(), peek(), empty()

    그래프 탐색의 예시

    int graph[MAX_N][MAX_N];
int stack[STACK_SIZE];
int top;

void dfs(int node) {
    bool visited[MAX_N] = {false};
    top = -1;
    stack[++top] = node; // push
  while (top != -1) {  // is_empty
      int curr = stack[top--]; // pop
        if (!visited[curr]) {
            visited[curr] = true;

            for (int next = 0; next < N; ++next) {
                if (!visited[next] && graph[curr][next]) {
                    stack[++top] = next; // push
                }
            }
        }
    }
}

    이진트리 탐색의 예시: stack을 출력을 위한 스택으로 활용한다는 점에 차이가 있다. 순회는 cur가 직접 돈다. visited를 써줄 필요가 없는 이유는 트리는 사이클이 없기 때문이다.

    typedef struct node_t{
    key_t key;
    node_t *left;
    node_t *right;
} node_t;

void dfs(node_t *root, void (*visit)(const node_t *)) {
    node_t *stack[STACK_SIZE] = {NULL}; // 포인터 배열 선언
    node_t *cur = root;
    int top = -1;

    while (top >= 0 or cur != NULL) {
        if (cur != NULL) {
            // go left
            stack[++top] = cur; // stack push
            cur = cur -> left;
        } else {
            // visit and go right
            cur = stack[top--]; // stack pop
            visit(cur);
            cur = cur -> right;
        }
    }
}

  • BFS : 시작점의 인접한 정점들을 먼저 차례로 방문한다. 그 뒤에 방문했던 정점으로부터 인접한 정점들을 차례로 방문한다.

    • Queue
    • FIFO 삽입된 원소 순서대로 나온다. (선입선출)
    • front := -1, rear := -1 변수를 사용하여 구현.
    • enqueue(), dequeue(), empty()
    int queue[QUEUE_SIZE];
int front = -1;
int rear = -1;
void enqueue(int val) {
    if (rear >= QUEUE_SIZE - 1) { overflow; }
    else {
        queue[++rear] = val;
    }
}

    void dequeue() {
    if (front == rear) { 반환할 게 없음 }
    else return queue[++front];
}
    • 원형큐 : 배열기반 큐는 사용할수록 공간이 버려지는게 많다는 문제가 발생. 이를 해소하기 위해 배열의 끝을 처음과 연결함. rear = (rear + 1) % QUEUE_SIZE front = (front + 1) % QUEUE_SIZE
    int graph[MAX_N][MAX_N];
int queue[QUEUE_SIZE];
int front;
int rear;
void bfs(int node) {
    bool visited[MAX_N] = {false};
    front = rear = -1;
    visited[node] = true;
    queue[++rear] = node;
    while(front != rear) {
        int curr = queue[++front];
        do_something_with(curr);
        for (int next = 0; next < N; ++next) {
            if (!visited[next] && graph[curr][next]) {
                visited[next] = true; // queue에 집어넣었으면 방문처리하는 것이 가능하다.
                queue[++rear] = next;
            }
        }
    }
}

    알아둘 점: visited를 설정하는 타이밍이 실제 방문을 했을 때가 아닌, queue에 넣었을 때라는 것을 기억하자. dfs는 스택에 중복된 원소를 넣을 수밖에 없었는데, 그 이유는 훨씬 전에 넣었던 원소가 언제 pop 할지 알 수 없었기 때문. 하지만 bfs는 중복 원소를 넣을 필요 없이 언제 그 원소가 dequeue되는지 알 수 있다.

    bfs는 가중치 없는 그래프에서는 경로의 길이를 구할 수 있다는 특징이 있다. 다른 정점을 한 번씩 방문할 때마다 dist 배열의 정점번호에 인접한 인덱스의 값 + 1 해주기만 하면 된다. dist[next] = dist[curr] + 1 이러면 dist는 시작노드로부터 모든 노드까지 이어지는 길이를 갖게 된다.

신장트리 (spanning tree)#

신장트리는 무방향 그래프 G의 정점을 모두 포함하고 최소 간선수를 갖는 서브그래프를 의미한다

신장트리를 만드는 법은 여러가지가 있다. 먼저 사이클을 일으키는 간선을 제거하는 방법이 있고, DFS, BFS를 순회하며 신장트리를 만드는 방법이 있다.

사이클 여부를 판단하는 방법은 바로 서로소 집합(disjoint set)의 Union Find를 통해 해결이 가능하다.

최소신장트리 (minimum spanning tree)#

최소신장트리는 가중치합이 최소가 되도록 만든 신장트리이다

대표적으로 prim algorithm과 kruskal algorithm {Minimum Spanning Tree}이 있다.
1197 최소 스패닝 트리 {boj}

이중 연결 요소 (Biconnected Components)#

다음 PR 참고