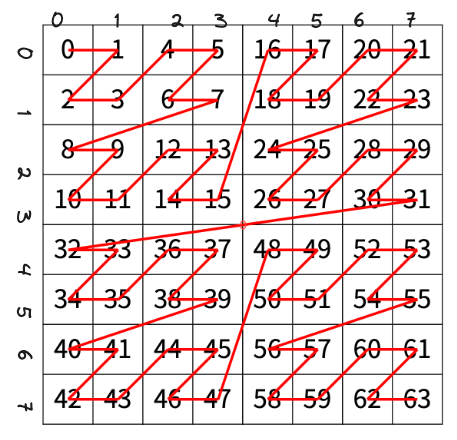
1074. Z

1차 시도#

Comparing result with enum in python를 참고하여 r, c값과 배열의 크기를 서로 비교해 몇사분면에 위치해 있는지를 판단하는 코드를 작성했다.

def sol_recur(n: int, dim: int, r: int, c: int, lo: int, hi: int) -> int:
    if dim == 0:
        return lo
    cell_size = 2 ** (2 * dim - 2)
    match (compare(r, 2 ** (dim - 1)), compare(c, 2 ** (dim - 1))):
        case (Cmp.Less, Cmp.Less):
            # 1분면에 있음
            hi = lo + cell_size
        case (Cmp.Less, Cmp.Greater):
            # 2분면에 있음
            lo += cell_size
            hi = lo + cell_size
        case (Cmp.Greater, Cmp.Less):
            # 3분면에 있음
            lo += cell_size * 2
            hi = lo + cell_size
        case _:
            # 4분면에 있음
            lo += cell_size * 3
            hi = lo + cell_size
    return sol_recur(n, dim - 1, r, c, lo, hi)


n, r, c = [int(e) for e in input().split()]

print(sol_recur(n, n, r, c, 0, 2 ** (2 * n)))

하지만 결과는 칼같이 오답이었다. 😞

이유로 하여금 match 안에서 r, c값을 잘못 비교한 게 아닐까 싶기는 한데... 관심 Cell의 크기와 위치가 자꾸 바뀌니까 r, c도 계속 바꾸어야 함.

≤, <같은 equality도 고려해야겠구나

Greater | Equal#

≥ 사인이 없었기 때문에 계속 4분면으로 빠졌던 것이었다.

def sol_recur(dim: int, r: int, c: int, lo: int, hi: int) -> int:
    if dim == 0:
        return lo
    # 넓이와 변의 길이를 저장한다.
    side = 2**dim
    area = side**2
    # 각 분면의 넓이와 변의 길이를 저장한다.
    cell_side = side // 2
    cell_area = cell_side**2

    match (compare(r, cell_side), compare(c, cell_side)):
        case (Cmp.Less, Cmp.Less):
            # 1분면에 있음
            hi = lo + cell_area
        case (Cmp.Less, Cmp.Greater | Cmp.Equal):
            # 2분면에 있음
            lo += cell_area
            hi = lo + cell_area
            c -= cell_side
        case (Cmp.Greater | Cmp.Equal, Cmp.Less):
            # 3분면에 있음
            lo += cell_area * 2
            hi = lo + cell_area
            r -= cell_side
        case _:
            # 4분면에 있음
            lo += cell_area * 3
            hi = lo + cell_area
            r -= cell_side
            c -= cell_side
    return sol_recur(dim - 1, r, c, lo, hi)


if __name__ == "__main__":
    n, r, c = [int(e) for e in input().split()]

    print(sol_recur(n, r, c, 0, 2 ** (2 * n)))

2024-12-27 다시 돌아왔다#

TLDR#

계산이 잘 안 맞을땐 표를 세워가며 n 값을 하나씩 늘려가며 변수들의 값을 계산해보는 습관을 가져보자. 한 번 말리니까 끝도 없이 시간이 흘러갔다.

n	size of array	size of part
1	4	1
2	16	4
3	64	16
k	\(2 ^ {2 k}\)	\(2^{2(k-1)}\)

Snippet#

def bound_idx(n: int, r: int, c: int) -> int:
    """
    0 1
    2 3
    """
    m = n - 1
    if r < 2**m and c < 2**m:
        return 0
    if r < 2**m and c >= 2**m:
        return 1
    if c < 2**m and r >= 2**m:
        return 2
    return 3


def order_of(n: int, bound_idx: int) -> int:
    """
    사분면 하나의 크기는 2**2n / 4 이기 때문에
    2 ** (2 * (n - 1)) 이라는 공식이 나왔다.
    """
    return bound_idx * (2 ** (2 * (n - 1)))


def normalize(n: int, r: int, c: int) -> tuple[int, int]:
    """
    normalize current position (r, c) into range([[0, 2**(n-1)], 2**(n-1)])
    """
    m = n - 1
    next_r = r if r < 2**m else r - 2**m
    next_c = c if c < 2**m else c - 2**m

    return (next_r, next_c)


def main(n: int, r: int, c: int) -> int:
    """
    2**n BY 2**n 배열에서 재귀Z 모양으로 방문할 때 r,c 를 몇번째에
    방문하는가?
    """
    bound = bound_idx(n, r, c)

    if n == 0:
        return 0

    order = order_of(n, bound)
    next_r, next_c = normalize(n, r, c)

    order += main(n - 1, next_r, next_c)

    return order


if __name__ == "__main__":
    n, r, c = map(int, input().split())
    print(main(n, r, c))

Sample Input & Expected Output#

Input#

Expected Output#