문제#

길이가 n인 수열 \(a_0, a_1, \cdots, a_{n-1} (0 ≤ a_i ≤ 10^9)\) 에서 아래 두 가지 쿼리를 처리하는 프로그램을 작성하라

- 0 i x : \(a_i\) 를 x로 바꾼다. \((0 ≤ i ≤ n - 1, 0 ≤ x ≤ 10^9)\)

- 1 l r    :    \(a_i\) (l ≤ i < r) 를 번갈아가며 더하고 뺀 값을 출력한다. (0 ≤ l < r ≤ n)
                   범위를 만족하는 i의 개수가 홀수일 경우 \(a_l - a_{l+1} + a_{l+2}  - \cdots - a_{r-2} + a_{r-1}\) 를 출력하고
                   범위를 만족하는 i의 개수가 짝수일 경우 \(a_l - a_{l+1} + a_{l+2}  - \cdots + a_{r-2} - a_{r-1}\) 를 출력하라.

[입력]
첫 번째 줄에 테스트 케이스의 수 T 가 주어진다.

각 테스트 케이스의 첫 번째 줄에는 배열의 길이 n\((1 ≤ n ≤ 10^5)\)과 쿼리의 개수 q\((1 ≤ q ≤ 10^5)\)가 주어진다.
두 번째 줄에는 배열 a가 주어진다.
세 번째 줄부터 q개 줄에 걸쳐 쿼리가 주어진다.

[출력]
각 테스트 케이스마다 1번 쿼리의 결과를 공백으로 구분하여 출력한다.

입력

출력

#1 3 3 9 -3  
#2 5 5

sol1 [Fail]#

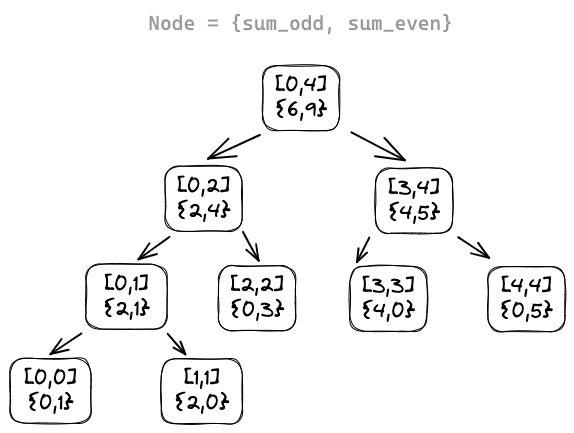
번갈아가며 더하고 뺀 결과를 트리에 넣고 쿼리가 들어오면 해당 구간에 있는 노드를 더하거나 빼서 리턴한다. 아래의 그림은 Seq = {1,2,3,4,5}일때의 세그먼트 트리이다.

![[Pasted image 20230216150837.png]]

/**add two child value*/
constexpr static elem_t _do_add(celem_t &left_child, celem_t &right_child,
                                cuint start, cuint end) {
  cuint mid = (start + end) / 2;
  if ((mid - start) % 2 == 0) {
    // even
    return left_child - right_child;
  } else {
    // odd
    return left_child + right_child;
  }
}

static Box<celem_t> _jagged_sum(Arr const &tree, cuint left, cuint right, //
                                uint node, uint start, uint end) {
  if (right < start || end < left) { // invalid range
    return Box<celem_t>::empty();
  }
  if (left <= start && end <= right) { // perfect range
    return Box<celem_t>(tree[node]);
  }
  // 두 노드에 걸쳐있는 경우
  uint mid = (start + end) / 2;
  auto left_child = _jagged_sum(tree, left, right, _left(node), start, mid);
  auto right_child = _jagged_sum(tree, left, right, _right(node), mid + 1, end);
  // merge
  if (left_child.contains && right_child.contains) {

    return Box<celem_t>(
        _do_add(left_child.get(), right_child.get(), start, end));
  } else if (!left_child.contains && !right_child.contains) {

    return Box<celem_t>::empty();
  } else {

    return left_child.contains ? left_child : right_child;
  }
}

/**
@breif: 재귀적으로 tree를 초기화.
@param:
  - data: 원본 배열
  - n: 원본 배열의 크기
  - node: tree의 노드의 인덱스
  - start: tree의 범위 시작 - inclusive
  - end: tree의 범위 끝 - inclusive
*/
static void _init(Arr const &data, Arr &tree, uint node, uint start, uint end) {
  if (start == end) { // leaf node
    tree[node] = data[start];
    return;
  }
  // recursive
  auto mid = (start + end) / 2;
  _init(data, tree, _left(node), start, mid);
  _init(data, tree, _right(node), mid + 1, end);
  // set current node
  tree[node] = _do_add(tree[_left(node)], tree[_right(node)], start, end);
}

/**
@breif: 재귀적으로 업데이트를 수행하며 연관 노드들을 같이 수정한다.
*/
static void _update(Arr &tree, cuint idx, celem_t value, uint node, //
                    uint start, uint end) {
  if (idx < start || end < idx) { // idx는 이 노드에 없다.
    return;
  }
  if (start == end) { // leaf node
    tree[node] = value;
    return;
  }
  uint mid = (start + end) / 2;

  // idx가 포함된 구간을 가지고 있는 자식노드만 순회하면 된다.
  _update(tree, idx, value, _left(node), start, mid);
  _update(tree, idx, value, _right(node), mid + 1, end);

  // 현재 노드에 가해질 변화 적용
  tree[node] = _do_add(tree[_left(node)], tree[_right(node)], start, end);
}

/**INTERFACES*/

/**data를 세그먼트 트리로 변환한다.*/
inline void init(Arr const &data, cuint n) { _init(data, _tree, 1, 0, n - 1); }

/**data[idx] := value */
inline void update(cuint idx, celem_t value, cuint n) {
  _update(_tree, idx, value, 1, 0, n - 1);
}

/**
@breif:
  [left, right-1] 범위의 i에 대하여 a_i를 번갈아가며 더하고 뺀 값을 출력한다.
*/
inline elem_t jagged_sum(cuint left_inclusive, cuint right_exclusive, cuint n) {
  return _jagged_sum(_tree, left_inclusive, right_exclusive - 1, 1, 0, n - 1)
      .get();
}

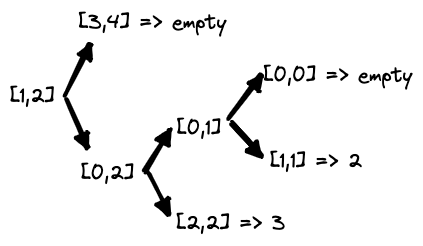
인터페이스 jagged_sum 을 보자. 만약 사용자가 jagged_sum(1,3)을 호출했다고 가정했을 때 콜스택은 다음과 같이 불릴 것이다. 1. _jagged_sum(3, 4) => empty() 2. _jagged_sum(0, 2) 3. _jagged_sum(0, 1) 4._jagged_sum(0, 0) => empty()5._jagged_sum(1, 1) => 26._jagged_sum(2, 2) => 3`

따라서 _jagged_sum(0,1) = 2 가 될 것이다. 이제 _jagged_sum(0, 2)를 구해보자.
left_child = _jagged_sum(0,1) = 2
right_child = _jagged_sum(2,2) = 3
_do_add(left_child, right_child, start: 0, end: 2) 에서 문제가 터진다. sol1은 언제 더하고 언제 뺄지를 결정하기 위해 start, end 변수를 활용한다. mid - start 가 짝수이면 left - right를, 홀수이면 left + right를 계산하는 식이다. 하지만 이것은 틀렸다. 직접 종이에 풀었을 때 직관적으로 (1,1)에서 (2,2)를 빼서 -1이 나와야 하지만 사실 _do_add 가 봤을 땐 (0,1)과 (2,2)가 들어온 것으로 생각하고 (2,2)에서 (0,1)을 빼게 된다. 따라서 1이 나오게 되는 것이었다.

최종 계산은 마지막에 진행하기 위해 나는 문제를 처음부터 다시 풀어야만 했다.

sol2 [Pass]#

이번엔 아예 홀수번째 원소들의 부분합, 짝수번째 원소들의 부분합을 따로 계산해 저장한 다음 쿼리시 일단 그냥 무지성으로 더한 뒤에 홀수번째에서 짝수번째를 뺄지, 반대로 할지 결정하도록 만들어 보았다.

Seq = {1,2,3,4,5}일때 예시:

constexpr bool _even(uint n) { return n % 2 == 0; }
constexpr bool _odd(uint n) { return !_even(n); }

struct Node {
  elem_t sum_odd{};
  elem_t sum_even{};
  constexpr explicit Node(elem_t sum_odd, elem_t sum_even)
      : sum_odd{sum_odd}, sum_even{sum_even} {}
  constexpr Node() = default;
  constexpr static Node even(elem_t elem) { return Node(0, elem); }
  constexpr static Node odd(elem_t elem) { return Node(elem, 0); }
};
inline Node operator+(Node const &lhs, Node const &rhs) {
  return Node(lhs.sum_odd + rhs.sum_odd, lhs.sum_even + rhs.sum_even);
}
inline Node operator-(Node const &rhs) {
  return Node(-rhs.sum_odd, -rhs.sum_even);
}
inline Node operator-(Node const &lhs, Node const &rhs) { return lhs + (-rhs); }
inline bool operator==(Node const &lhs, Node const &rhs) {
  return lhs.sum_odd == rhs.sum_odd && lhs.sum_even == rhs.sum_even;
}

template <typename T> using Arr = std::array<T, LEN>;

static Arr<Node> _tree;

/**INTERNALS*/

/**
tree를 세그먼트 트리 구조로 초기화 한다.
*/
static void _init(std::array<elem_t, N> const &data, Arr<Node> &tree, uint node,
                  uint start, uint end) {
  if (start == end) { // leaf node
    tree[node] =
        _even(start) ? Node::even(data[start]) : Node::odd(data[start]);
    return;
  }
  auto mid = (start + end) / 2;
  _init(data, tree, _left(node), start, mid);
  _init(data, tree, _right(node), mid + 1, end);
  // merge two children
  tree[node] = tree[_left(node)] + tree[_right(node)];
}

static void _update(Arr<Node> &tree, cuint idx, celem_t value, uint node,
                    uint start, uint end) {
  if (idx < start || end < idx) { // wrong node
    return;
  }
  if (start == idx && end == idx) { // leaf node
    tree[node] = _even(start) ? Node::even(value) : Node::odd(value);
    return;
  }
  auto mid = (start + end) / 2;
  _update(tree, idx, value, _left(node), start, mid);
  _update(tree, idx, value, _right(node), mid + 1, end);
  // merge
  tree[node] = tree[_left(node)] + tree[_right(node)];
}

/**
여기에서는 단순히 노드들을 더한 결과를 리턴한다.
*/
static Node _sum(Arr<Node> const &tree, cuint left, cuint right, uint node,
                 uint start, uint end) {
  if (end < left || right < start) { // wrong node
    return Node(0, 0);
  }
  if (left <= start && end <= right) { // node inside the range
    return tree[node];
  }
  // overlapped range
  auto mid = (start + end) / 2;
  Node left_child = _sum(tree, left, right, _left(node), start, mid);
  Node right_child = _sum(tree, left, right, _right(node), mid + 1, end);
  return left_child + right_child;
}

/**INTERFACES*/

/**data를 세그먼트 트리로 변환한다.*/
inline void init(std::array<elem_t, N> const &data, cuint n) {
  _tree.fill(Node());
  _init(data, _tree, 1, 0, n - 1);
}

/**data[idx] := value */
inline void update(cuint idx, celem_t value, cuint n) {
  _update(_tree, idx, value, 1, 0, n - 1);
}

/**
@breif:
  [left, right-1] 범위의 i에 대하여 a_i를 번갈아가며 더하고 뺀 값을 출력한다.
*/
inline elem_t jagged_sum(cuint left_inclusive, cuint right_exclusive, cuint n) {
  Node sum = _sum(_tree, left_inclusive, right_exclusive - 1, 1, 0, n - 1);
  return _even(left_inclusive) ? sum.sum_even - sum.sum_odd
                               : sum.sum_odd - sum.sum_even;
}

마찬가지로 사용자가 jagged_sum(1,3)을 호출했다고 가정하자. 콜 스택 호출 순서는 그대로이므로 또 적지는 않겠다.

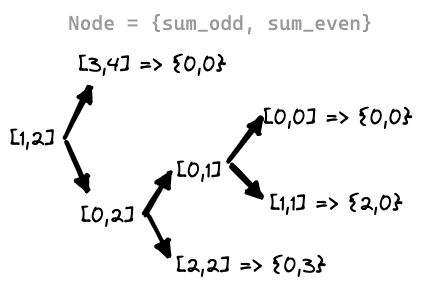
sum(0,2) = {2,3}
sum(1,2) = {2,3}

그냥 더하는 것에 불과하기 때문에 노드간에 합은 쉽게 구할 수 있다. 이제 jagged_sum의 마지막 줄을 보자. 이제 우린 left가 짝수인지만 확인하면 누구에서 누구를 빼야할지 쉽게 알 수 있다. 위의 예제의 경우 start = 1, 홀수 이므로 sum_odd에서 sum_even를 빼주면 된다. 따라서 2 - 3 = -1이 나오게 된다.

return _even(left) ? sum_even - sum_odd
                   : sum_odd - sum_even