No. 25 중간값 구하기

---

풀이

한시간 고민했지만 문제를 풀 수 없었다. 결국 다른 사람의 풀이를 봤는데...

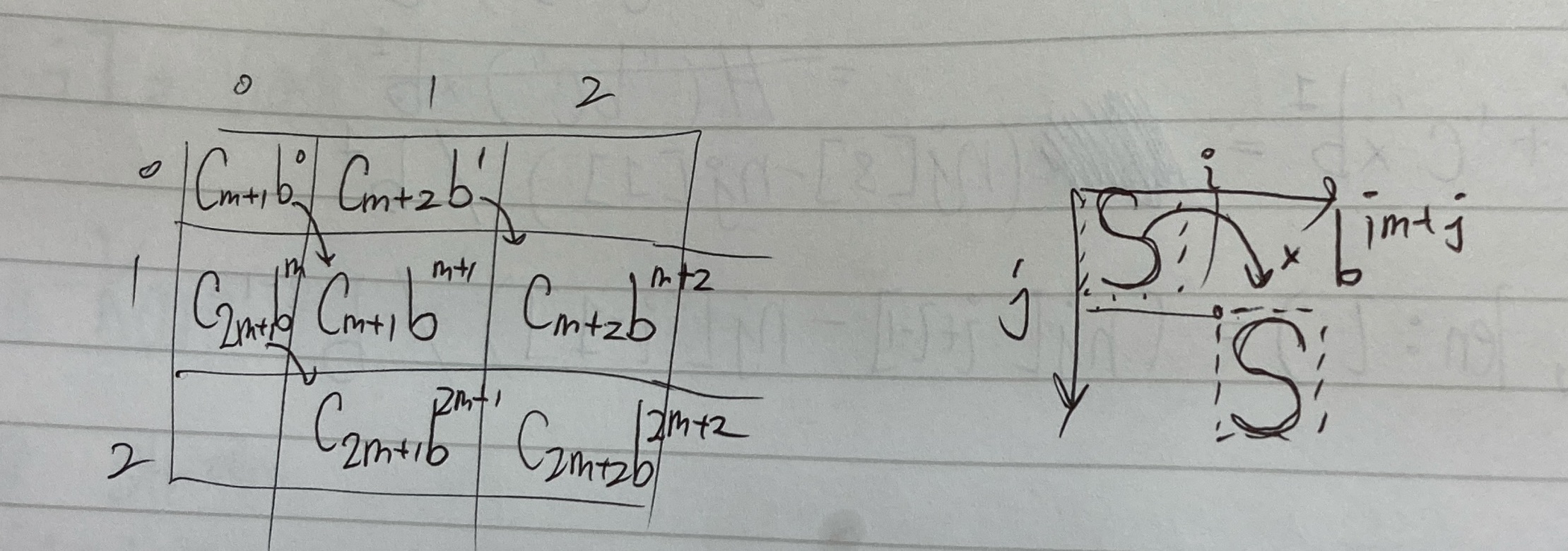
maxheap과 minheap을 양 옆으로 붙여버리면 되는 것이었다. 정확히 말하자면 두 가지 조건을 만족시키게만 만들면 된다. 1. maxheap.size == minheap.size 2. maxheap.top < mid && mid < minheap.top

Code

/**
sorted:

1,2,3,4,5,6,7,8,9
........^
maxheap...minheap

언제나
mid < minheap.front() && maxheap.front() < mid &&
minheap.size() == maxheap.size()를 만족한다.
*/
class Solution {

  priority_queue<elem_t, vector<elem_t>, less<elem_t>> m_maxheap{};
  priority_queue<elem_t, vector<elem_t>, greater<elem_t>> m_minheap{};
  elem_t m_mid;

public:
  explicit Solution(elem_t mid) : m_mid{mid} {}

  /**add1, add2를 추가한 뒤 중간값을 리턴한다.*/
  elem_t add(elem_t add1, elem_t add2) {
    m_mid < add1 ? m_minheap.push(add1) : m_maxheap.push(add1);
    m_mid < add2 ? m_minheap.push(add2) : m_maxheap.push(add2);
    // minheap, maxheap의 size를 맞춤과 동시에 mid를 수정한다.
    while (m_minheap.size() < m_maxheap.size()) {
      m_minheap.push(m_mid);
      m_mid = m_maxheap.top();
      m_maxheap.pop();
    }
    while (m_maxheap.size() < m_minheap.size()) {
      m_maxheap.push(m_mid);
      m_mid = m_minheap.top();
      m_minheap.pop();
    }
    return m_mid;
  }
};