Doit 자료구조와 함께 배우는 알고리즘 기초 파이썬 편

swjungle 🤖의 일환으로 학습한 자료를 정리한 문서입니다.

구조적 프로그래밍: 순차구조(sequential)와 선택(selection)구조, 반복(iteration)구조
- 순차: 한 문장씩 처리
- 선택: 조건에 따라 실행 흐름 변경
- 반복: 조건이 성립하는 동안 주어진 구간의 코드를 반복
  - 카운터용 변수 (cnt, counter, ...): 반복문을 제어할 때 사용되는 변수
형변환 to integer, floating point
- int(문자열, 진수), float(문자열)
헤더와 스위트(suite) {python}
What is the algorithm?
- 문제를 해결하기 위해 기술된 일련의 실행절차
Decision Tree (결정트리)
- 세 정수 a, b, c의 대소관계조합을 모두 나열해보면 트리형태를 띄게 된다. 이것을 결정트리라고 부름.
DRY (Don't Repeat Yourself)
- DRY 메커니즘의 예시: 하드코딩을 피하라 reverse를 사용해야 하는 이유 {django}
- 논리적으로 일치하는 분기문을 갖다 쓰지 말라. if a < b: ... \n elif b >= a: ... 이딴거 쓰지 말라는 거임 p.25
- 9999번 A 분기에 들어가고 1번 B 분기에 들어갈거면 if 쓰지 말라. p.38
  - 파이썬은 배열을 각각 리스트와 튜플로 구현할 수 있다. 리스트는 변경이 가능하고, 튜플은 변경이 불가하다는 차이가 존재하다.
  - [?] p.42 ~ p.44 for 문 안에 있는 if문이 무의미한 경우 (1억번 중 1억번 같은 브랜치) 파이썬은 내부적으로 분기예측을 통해 최적화를 하는가? ^8px73d
if구문에서 else를 쓰지 않으면 내부적으로 else: pass가 숨어있다.
연산자와 피연산자, operator, operand. 용어파악
- 삼항 연산자 (ternary operator) : x if x < y else y
swap: a, b = b, a 개쩔지 아니한가 : ~~사실 튜플 공간을 만들어 쓰는거라서... 변수를 하나 생성하여 스왑하는 것보다 비효율적임~~ 튜플은 레퍼런스를 담을 공간이다.
str * 연산자는 문자열을 복제하여 리턴한다.
파이썬의 모든 변수는 값을 저장하지 않는다. p.56
- 파이썬에서의 모든 건 객체이고, 변수는 그 객체를 참조하는 참조자에 불과. 엄밀한 의미에서의 포인터는 아니지만 고유식별번호가 있어 id()를 사용하여 이를 찍어볼 수 있다.
[?] 파이썬이 언제 메모리를 비우는가??
[?] range 음수 갭을 주었을 때 실험해보자.

Chapter02 기본 자료구조와 배열#

DRY (Don't Repeat Yourself)
- 배열은 프로그램을 덜 수정하기 위해 도입된 개념이다. p.62 집계, 인덱싱, 정렬, 해싱 등을 활용할 때 세부적이지 않은 사항인 원소의 개수에 영향을 최소화할 수 있다.
tuple(), list() 함수를 사용하면 순회 가능한 모든 놈들을 전부 리스트로 만들 수 있다.
튜플은 불변성에 높은 가치를 두어야 할 것 같다.
누적 대입: int, str 같은 리터럴들은 값이 변하지 않는다. 1이 갑자기 2가 되거나 하지 않는다는 것이다. 그렇다면 우리가 리터럴을 저장한 변수에 +=과 같은 연산을 통해 값이 변하게 만드는 것은 무엇이냐? 단순히 리터럴 1에서 리터럴 2로 참조자를 변경한 것에 불과하다.
- [!] 그건 그렇고 무한한 정수를 전부 메모리에 담을 수 없는데, 정수형 리터럴은 그럼 일종의 바운더리가 있는걸까? ==> 맞기는 한데, 바운더리의 범위는 IDE나 인터프리터에 따라 얼마든지 달라질 수 있다.
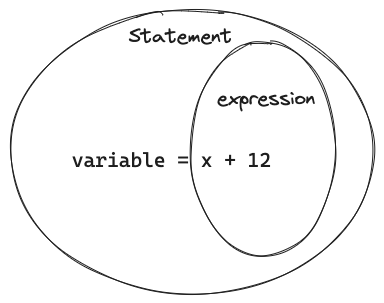
statement and expression
- statement: 출력값, 자료형이 없음. x = 2와 같은 대입 연산자의 결과는 값을 리턴하지 않는다.
- expression: 출력값, 자료형이 있음. x + 17은 값을 리턴한다. 리턴한 값을 함수 인자에 넣을 수도 있고, statement에 넣을 수도 있다.
자료구조 (Data Structure)는 데이터가 모여있는 구조이다. 데이터가 어떻게 모여있는지는 궁금해 하지 않도록 적당히 추상화를 했다. 따라서 자료구조는 추상 자료형 (Abstract Data Type)이다.
- [?] abstract data type과 interface, class와의 차이

배열의 대소, 등가관계

[1, 2, 3] == [1, 2, 3]
[1, 2, 3] < [1, 2, 4]
[1, 2, 3] < [1, 2, 3, 5]

typing.Sequence : list, bytes, bytearray, string, tuple
custom iterator with iter in python
call by object reference {python}

소수 나열 p.97 예상시간 15min
교재에 나온 방식이 내가 알고 있던것과는 사뭇 다르다. 적어도 책에서는 아리스토테네스의 체를 사용하지 않는다. 수도코드를 작성해보면..
```
primes = [2]
for n in range(3, MAX, 2):
    for p in primes:
        if n % p == 0:
            break
    else:
        primes.append(p)
```

for문 끝나자마자 else가 나타나는 것은 처음 봤다. Why does python use 'else' after for and while loops

어쨌든 소수를 찾을때엔 primes의 모든 원소를 찾아야 하니 \(\Pi(N)\)정도의 시간이 걸린다. Prime Counting Function 참고{wiki} 조금만 더 최적화를 한다면 굳이 primes의 모든 원소를 찾을 필요는 없고, 제곱근 정도의 시간만 소요되게 만들 수 있겠다. 그리고 MAX까지 달려갈 때 모든 짝수를 제외할 수 있으므로.... 전체적으로 보았을 때 대충..

\[ O(\frac{\Pi(\sqrt{N})}{2} \cdot \frac{N}{2})=O(N\Pi(\sqrt{N})) \]

이...렇......게? 되려나? \(\Pi\)가 대충 로그정도의 속도를 가지고 있다고 하니까 조금만 더 멍청하게 생각한다면 \(O(N \log{\sqrt{N}})\) 정도.....?? 그냥 에라토스테네스의 체를 사용해서 메모리는 많이 먹어도 \(O(N)\)에 끝내는 방법이 더 현명해 보이기도 하지만 일단 머리속에 입력은 해두자.

Chapter03 검색 알고리즘 :: 이진검색 / 이분검색#

이진검색 p.120 예상시간 30min

이분탐색 헷갈리지 않게 구현하기 {최백준}

binary search를 활용한 lower upper bound 그리고 parametric search까지

파이썬에선 index() 함수로 리스트, 튜플 내 원소 검색을 수행할 수 있다.

meta: 2023-08-12T15:00:41
- 지금까지 나간 진도,
  - Ch02 p.61 ~ Ch03 p.130
- 15:00~17:00 스프린트에서 나갈 진도,
  - Ch05-03 하노이의 탑 p.200
  - Ch05-04 8퀸 문제 p.204
  - Ch06-1 정렬 알고리즘 p.219
  - Ch06-02 버블 정렬 p.221
- 오늘 밤까지 끝낼 진도,
  - Ch06-03 단순선택정렬 p.237
  - Ch06-04 단순삽입정렬 p.240
  - from: Ch06-05 셀 정렬 p.247
  - to: Ch06-09 도수 정렬 p.297
- 일요일까지 끝낼 진도
  - from: Ch09-01 트리 구조 p.377
  - to: Ch09-02 이진트리와 이진 검색 트리 p.382

Chapter05 재귀 알고리즘#

문제풀이는 전부 algorithms 페이지에서 진행함.

하노이의 탑: p.200
8퀸 문제: p.204
N-Queen {boj}

8개의 퀸이 서로를 잡을 수 없도록 8 * 8 체스판에 배치하시오

Z {1074} {boj} {재귀}
meta
- 본격적으로 읽기속도가 더뎌지기 시작했다. 기초개념에서 시간을 많이 쏟지는 않았을까 걱정이 되기는 하지만 그래도 몰랐던 것들도 많이 알게 되고, 내가 알고 있던 것들도 많이 공유하고 해서 최선을 다했다는 생각만 가지고 가자.
- 예상과는 다르게 책을 주말 안에 다 못 읽을 것 같다. 현재 재귀쪽에서 머물면서 관련 문제들을 몽땅 풀었고, 그래도 브루트포스/전수조사를 재귀함수로 푸는 것에 대한 감은 다시 되찾은 것 같다.
- 지금 팀원 한 분이 몸이 아파서 자리에 없다. 진도를 뺄 상황은 아닌 것 같은데, 열심히 문제를 풀어야 겠다.

Chapter06 정렬 알고리즘#

안정성(stability): 정렬을 수행한 후에도 값이 같은 두 원소들의 순서가 변하지 않는 경우, 해당 정렬을 안정적이라고 말할 수 있다.
내부정렬과 외부정렬: 하나의 메모리 공간 안에서 모든 정렬을 수행할 경우, 내부정렬이라고 하고, 그렇지 않은 경우(정렬할 데이터의 양이 너무 많은 경우) 파일 시스템을 활용해가며 정렬을 수행하게 되는데, 이것을 외부정렬이라고 부른다.
버블정렬 p.221
- 단순 버블정렬 구현만 보여준 게 아니라 한 바퀴 순회할 때마다 이미 정렬이 된 부분에 대하여 비효율적인 반복을 피하기 위해 최적화 작업을 수행하는 모습이 나온다. 이게 아니었으면 i = 0, 1, 2, ... 순으로 진행했을텐데, 스왑을 안했다는 소리는 곧 정렬이 완료됐다는 소리나 마찬가지기 때문이다.
```python from typing import MutableSequence

def bubble_sort(a: MutableSequence) -> None: """버블정렬(스캔 범위를 제한)""" n = len(a) k = 0 while k < n - 1: last = n - 1 for j in range(n-1, k, -1): # 거꾸로 버블소트 if a[j - 1] > a[j]: a[j - 1], a[j] = a[j], a[j - 1] last = j # 바로 여기서 점프할 인덱스를 지정한다 k = last ```
- 칵테일 셰이커 정렬이라고, 거의 완료된 정렬 [9, 1, 2, 3, 4, 5]에 대하여 위의 코드는 사실 \(N^2\)의 시간복잡도를 보인다. 왜냐면 점프할 인덱스가 항상 한 칸씩만 당겨오기 때문이다. 그래서 한 번은 우에서 좌로 훑고, 다른 한 번은 좌에서 우로 훑어 해당 현상을 없앤다.
- 단순 선택 정렬 p.237
- 순회를 하면서 매번 가장 작은 원소를 [0]번째 원소와 스왑. 덕분에 unstable하다.
- 단순 삽입 정렬 p.240
- 정렬이 완료된 구간을 늘려나가는 방식의 정렬방법.
```
from typing import MutableSequence

def insertion_sort(a: MutableSequence) -> None:
    n = len(a)
    for i in range(1, n):
        j = i
        tmp = a[j] # 스왑하지 않고 tmp로 값을 보관하는 이유는 a[j, j-1, ...] 자리에 그대로 값을 박을거기 때문이다.
        while j > 0 and tmp < a[j-1]:
            a[j] = a[j-1]
            j -= 1
        # 이 아래는 볼 필요도 없이 정렬되어있다.
        a[j] = tmp
```
이진 삽입 정렬 p.244
- 단순 삽입 정렬 알고리즘은 정렬되지 않은 구역을 순회하며 책을 꽂듯이 삽입했다면, 이진 삽입 정렬은 정렬된 구역을 이진탐색하여 그 사이를 비집고 밀어넣는다.
- 하지만 bisect.insort 문서에 조언에 따르면, 검색에 아무리 \(O(\log {N})\) 시간이 걸렸더래도 삽입하는 데에 \(O(N)\)의 시간이 소요되기 때문에 주의하라고 한다.
셸 정렬 p.247
- 단순 삽입 정렬의 장점을 살리면서 많은 데이터 이동을 줄이기 위해 고안된 방법
퀵 정렬 p.257
- Quick Sort
- 20230518 estsoft - python - tree -- LIS -- selection sort -- insertion sort -- merge sort -- quick sort#quick sort
병합 정렬 p.277
- 20230518 estsoft - python - tree -- LIS -- selection sort -- insertion sort -- merge sort -- quick sort#merge sort
**힙 정렬 p.286
- [[Heap|힙]]
- 루트를 삭제하고 힙을 재구성
- heapify: bottom-up 방식으로 가장 아래에 있는 서브트리부터 차례로 힙 트리로 만든다.
도수 정렬(Counting Sort) p.297
- 누적도수분포표를 만든다 (누적 히스토그램)
- 정렬할 리스트를 순회하며 누적도수분포표가 가리키는 인덱스에 원소를 넣고 누적도수분포표의 값을 1 줄인다.
- profit 💵
- 아, 수 정렬하기 3 (Counting Sort)

Chapter04 스택과 힙#

Chapter09 트리#

tree 기초 graph 기초