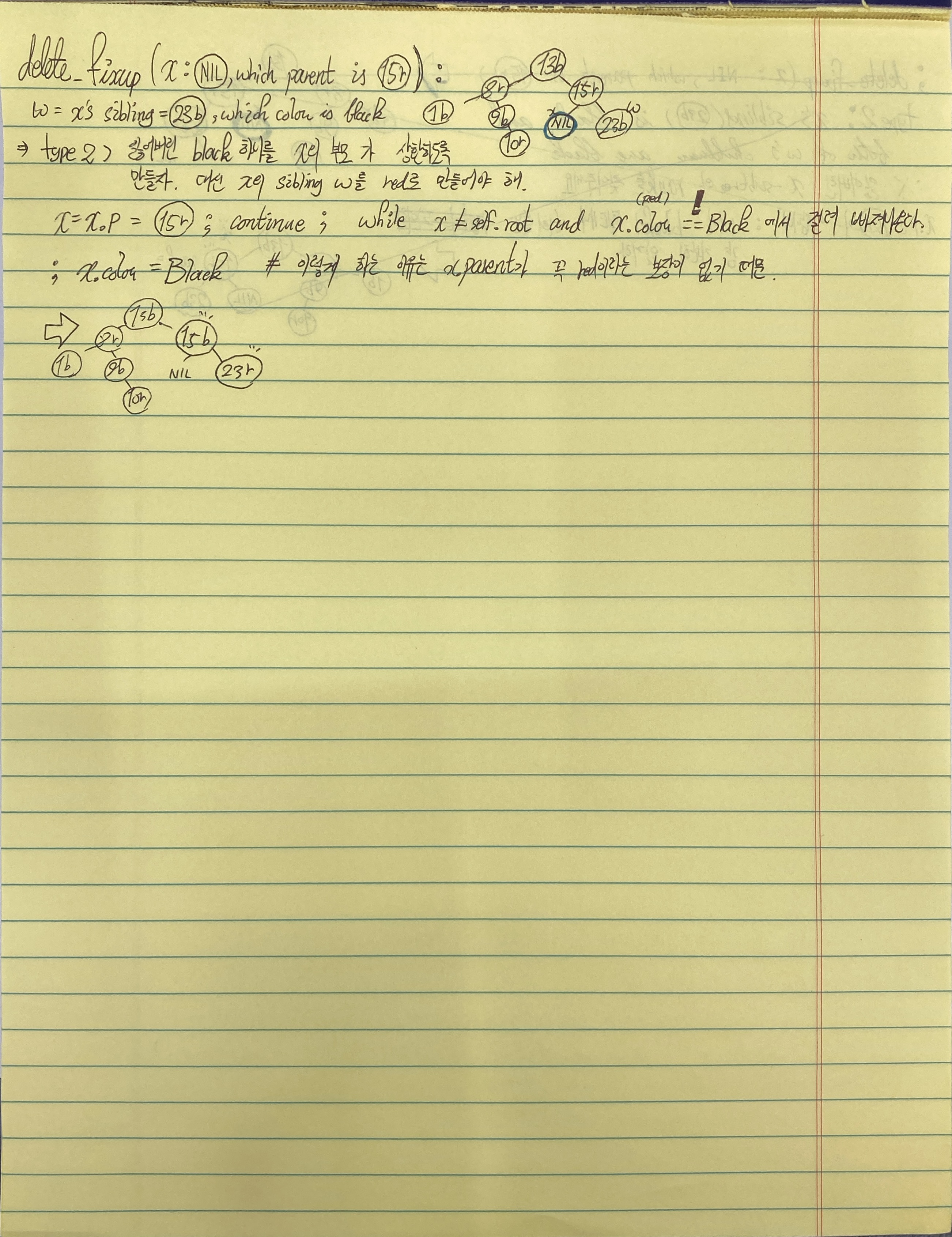이진검색트리 red black tree

parent link:
- 0011 Algorithms ♾️
- week 04 {swjungle} {Red Black Tree}
ChoiWheatley/swjungle-week-04 {GH}
참고하기 좋은 자료들
- CSLR Chapter 13 Red-Black Trees
- C로 쓴 자료구조론 - Horowitz, Sahni Anderson-Freed, 이석호 역 10.3 Red-Black Trees
- msambol/dsa/trees/red_black_tree.py {GH}
- redblack tree visualization tool
- linux 커널 rbtree 코드 {안쓰는 비트를 활용한 최적화}

이진검색트리 red black tree#

이진탐색트리를 먼저 구현하고 스스로 균형을 조절하는 RB-tree (Red-black tree) 트리를 만들어 보겠다.

height는 \(\lg{(n+1)}\) 보다 크거나 같고 \(2 \lg{(n+1)}\) 보다 작거나 같다.#

증명

이진트리에서 전체 노드의 개수를 \(n\) 이라고 하고 트리의 높이를 \(h\) 라고 하자. 포화이진트리일 경우 h에 대한 n이 최대일 때이므로 \(n \le 2^h - 1\) 이다. 따라서 \(\lg{(n+1)}\le h\)가 성립한다.
leaf 노드까지 만나는 black 노드의 개수를 \(r\)이라고 하자. RBTree의 제약조건 때문에 하나의 red 노드의 뒤에는 black 노드가 오게 된다. 그러므로 루트에서 외부노드로의 경로는 최소 \(r\)(모든 경로가 black), 최대 \(2r\)개(모든 경로가 black-red 반복)의 노드를 거치게 되므로 \(r \le h \le 2r\)이 성립한다.
r과 n의 관계는 포화이진트리의 모든 노드가 Black인 경우 최대이므로 \(2^{r} - 1 \le n\) 을 만족한다. 따라서 \(r \le \lg{(n + 1)}\)을 만족하며, 양변에 2를 곱하면 \(2r \le 2\lg{(n + 1)}\) 이므로 \(h \le 2\lg{(n + 1)}\)가 된다.

RBTree의 최대 높이는 \(2 \lg{(n+ 1)}\)이므로 \(O(h)\) 탐색시간 안에 수행하는 동안 최대 \(O(2\lg{(n+1)})\)이 필요하며, 따라서 RBTree 삽입,삭제 알고리즘의 시간복잡도는 \(O(\log{n})\)이 된다.

KEYWORDS#

keywords
- left rotate
- right rotate
- insert
  - insert_fixup
    - case1) ??r Z's uncle is red
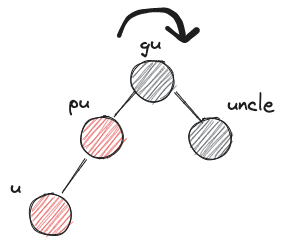
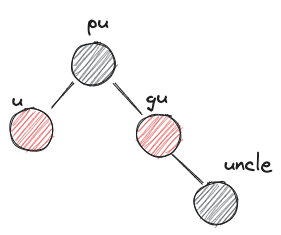
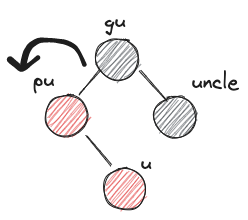
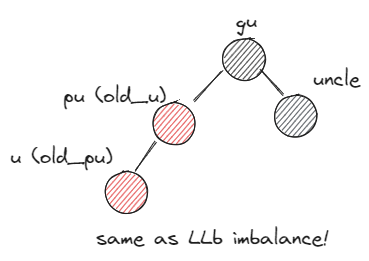
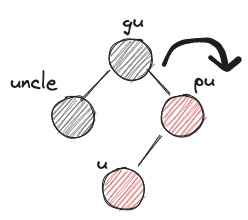
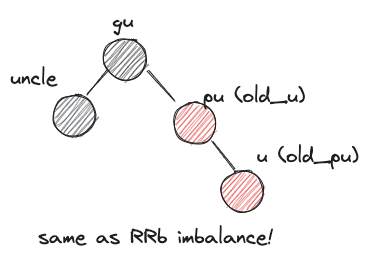
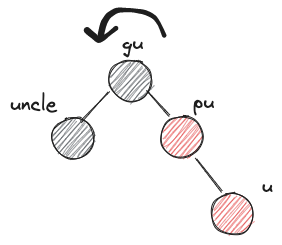
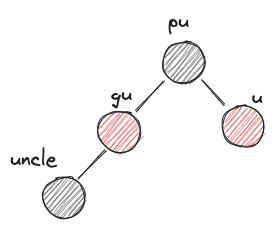
    - case2) LRb, RLb Z's uncle is black and Z's parent, grandparent form a triangle
    - case3) LLb, RRb Z's uncle is black and Z's parent, grandparent form a line
- deletion
  - transplant (u, v)
    - case1) u's parent is None
    - case2) u is u's parent's left child
    - case3) u is u's parent's right child
  - delete (x)
    - case1) left child is NIL
    - case2) right child is NIL
    - case3) both of children are not NIL
  - delete_fixup (x)
    - let w x's sibling
    - case1) w is red
    - case2) w is black, w's both children are black
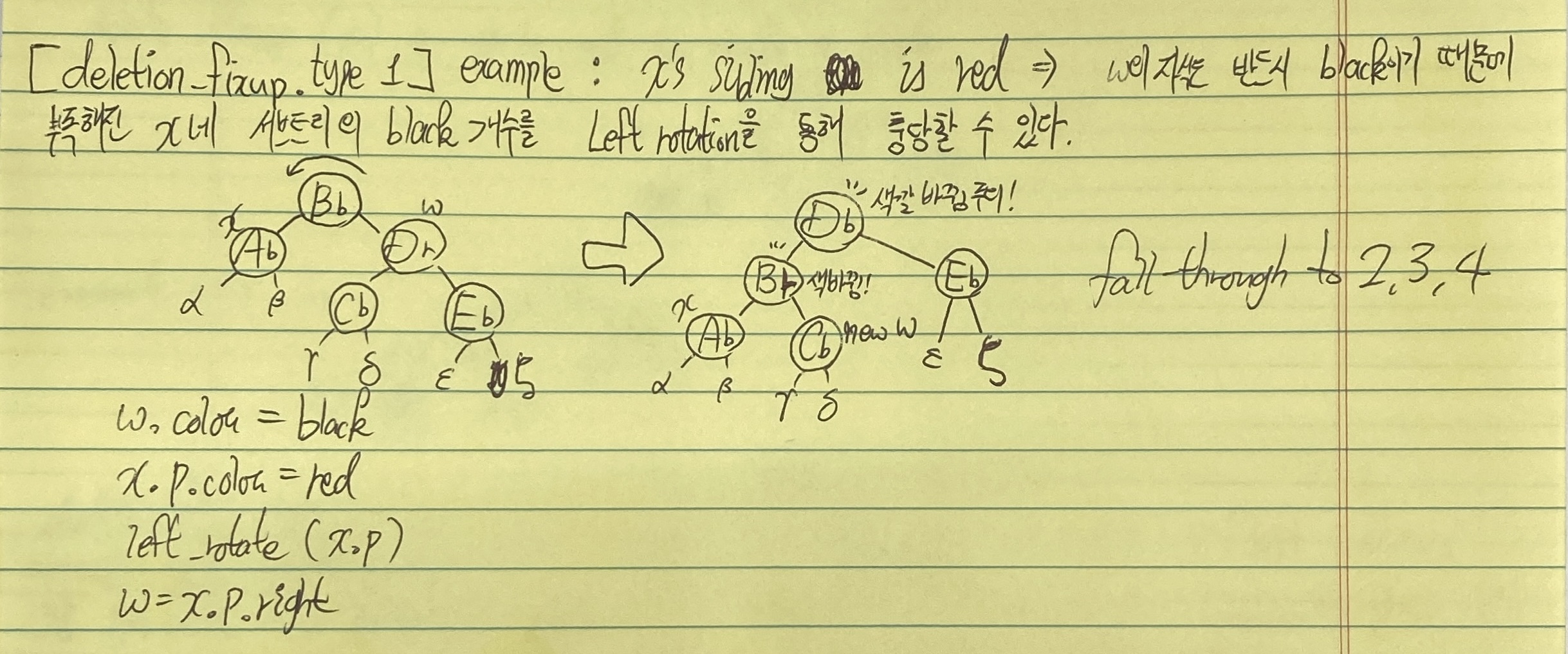
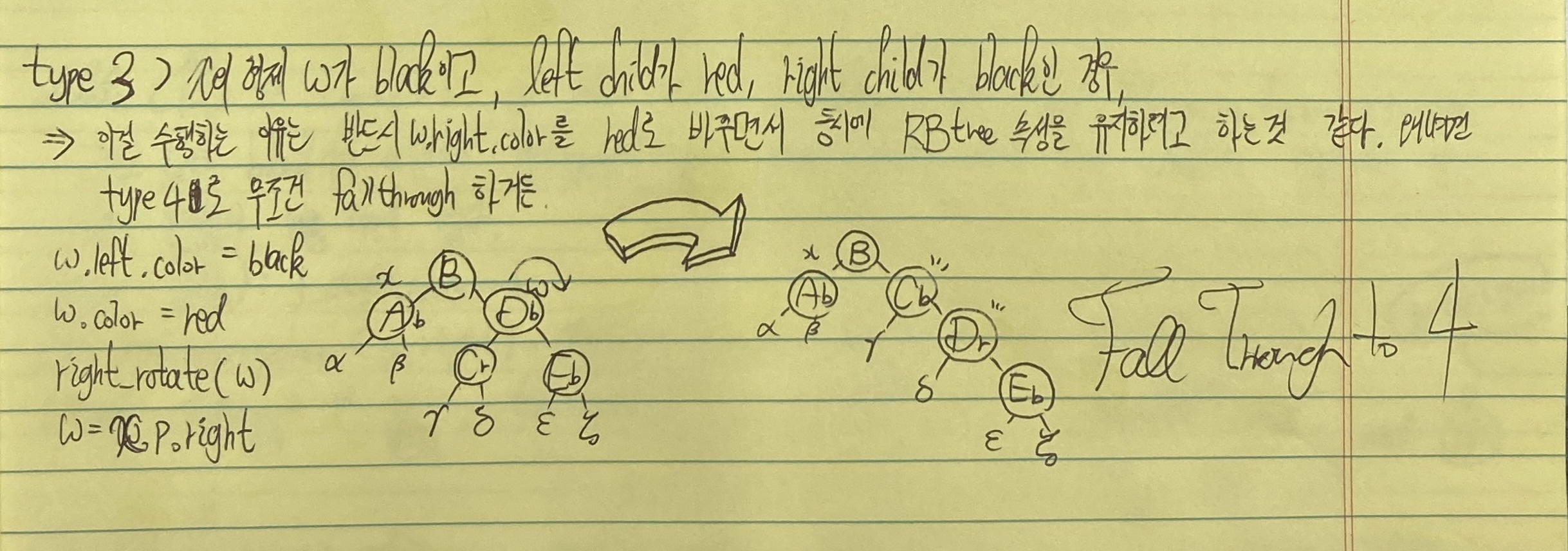
    - case3) w is black, w's left child is red, right child is black
    - case 4) w is black, w's right child is red
[x] questions
- duplicates를 처리하기 위해선 node_t에 count라는 속성을 추가해야 한다. 하지만 현재 프로젝트의 제약사항으로 "rbtree.c"만 수정해야 하는데, 정말로 node_t를 수정하지 않고 중복 원소를 처리하라는 것인가?
- (답변) 네, 가능합니다. 정렬된 list를 [1,1, 2, 2, 2, 3]과 같이 구현할 수도 있고 {1: 2개, 2: 3개, 3: 1개} 로 구현할 수도 있습니다만, 앞의 방식으로 구현하라는 이야기입니다.

RBTree 제약조건#

모든 노드는 RED 이거나 BLACK이다.
루트에서 리프노드로의 경로는 2개의 연속적인 RED 노드를 가질 수 없다.
루트에서 뻗어나가는 모든 경로의 BLACK 노드의 개수(rank)는 동일하다.

ADT#

ADT RBTree:
    objects: 공백이거나 루트노드, 왼쪽 노드, 오른쪽 노드로 구성되는 노드들의 유한집합, ordered set, multiset
    functions: 
        모든 t, t1, t2 ∈ RBTree에 대하여
        - RBTree new_tree() -> rbtree: 비어있는 트리 생성
        - delete_tree(tree): 트리의 메모리 반환
        - tree_insert(tree, key) -> node: tree에 key 추가, 추가한 노드의 주소 반환
        - elem_p tree_find(tree, key) -> node: 트리 안에 key 탐색 후 노드의 포인터 또는 NULL 반환
        - tree_erase(tree, ptr) -> node: 트리 내부의 ptr로 지정된 노드 삭제 후 메모리 반환
        - elem_p tree_min(tree) -> node: 트리 중 최소 값을 가진 노드의 포인터 반환
        - elem_p tree_max(tree) -> node: 트리 중 최대 값을 가진 노드의 포인터 반환
        - tree_to_array(tree, array_out, n): 
            - 트리의 내용을 key 순서대로 주어진 array로 변환. 
            - array의 크기는 n으로 주어지며, tree의 크기가 n보다 큰 경우 순서대로 n개 까지만 반환
            - array의 메모리 공간은 이 함수를 부르는 쪽에서 준비하고 그 크기를 세번째 인자로 알려줍니다.

tree_to_array(tree, arr_out, n)를 DFS 순회 코드의 callback함수를 사용하여 만들어 보려고 했으나 대차게 실패했다. 일단 C 자체에서 람다함수나 중첩 함수 선언같은걸 지원하지 않는데다, Callable 타입 객체를 만드는 것도 다른 언어에서는 어떻게 했는지 모르겠지만 C에서는 전역변수에 접근하는 것 말고는 다른 함수의 지역변수에 접근하는 것은 불가능해보였다.
2024-01-05 그거 PintOS 코드에서 영감을 얻은 void * aux 인자를 사용하여 스코프 내의 변수를 캡처하는 것이 가능할 것이다.

Helper Functions#

insert_case(u, parent, grandparent, uncle) -> LLr | LRr | RLr | RRr | LLb | LRb | RLb | RRb
rotate_left(x)
rotate_right(x)
transplant(u, v)
- u자리를 v로 대치하고 u 서브트리를 연결해제한다.
travel_bfs(T, callback)
- bfs 순회를 한다.
travel_dfs(T, callback)
- dfs 순회를 한다.
subtree_min(u)
- u 서브트리의 최솟값에 해당하는 노드를 리턴한다.
subtree_max(u)
- u 서브트리의 최댓값에 해당하는 노드를 리턴한다.

Insert#

새 노드는 언제나 red노드로 만들어 시작한다. 그 이유는 black 노드로 만들면 항상 RBTree 제약조건 3번 (모든 path로 향하는 black node의 개수가 동일하다)를 어기지만 red 노드로 만들면 RBTree 제약조건 2번 (연속하는 red 노드는 없다)를 어길 수도 있지만 어기지 않을 수도 있기 때문이다.

RBTree 제약조건을 어겼을 때 fixup을 해주어야 한다. 총 8가지 케이스가 있는데, 중복되는 것들이 있으므로 편하게 들어도 된다.

Imbalance Cases#

먼저 용어정리부터 하고 넘어갑시다

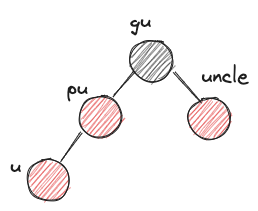
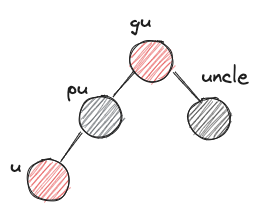
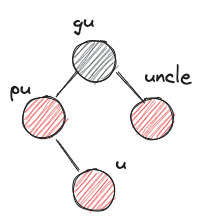
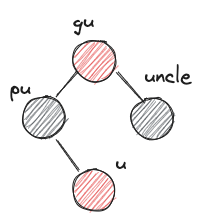
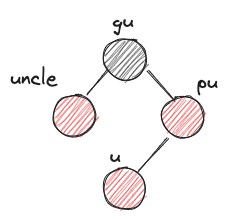
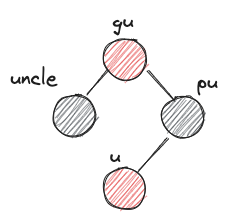
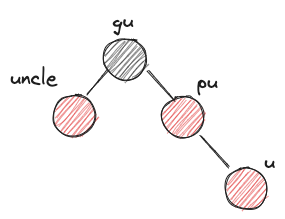
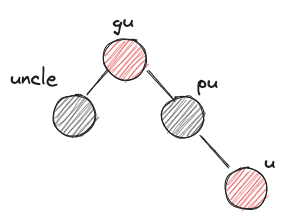
u: 새로운 노드
pu: u의 부모
gu: u의 조부모
uncle: gu의 다른 자식
XYz imbalance
- X, Y는 L 또는 R이다. 왼쪽에서부터 gu입장에서 pu의 위치, pu 입장에서 u의 위치를 나타낸다.
- z는 r 또는 b이다. uncle의 색상을 나타낸다.
XYr imbalance는 단순히 색깔만 바꿔주면 된다. gu의 색이 바뀌기 때문에 gu 노드의 부모와 그 상위 노드들 간에 RBTree 제약조건 2번을 어겼는지 여부를 검사해야 한다. 따라서 u를 gu로 바꿔 while 루프를 돈다.
- LLr
  - before:
  - after:
- LRr
  - before:
  - after:
- RLr
  - before:
  - after:
- RRr
  - before:
  - after:
XYb imbalance부터는 회전이 들어간다. 특히나 X,Y가 서로 다를땐 XXb 형식으로 회전한 다음 다시 XXb imbalance를 해결하는 것으로 fallthrough 한다는 점을 유의하자.
- LLb
  - before:
  - after:
- LRb
  - before:
  - after:
- RLb
  - before:
  - after:
- RRb
  - before:
  - after:

Delete#

summary#

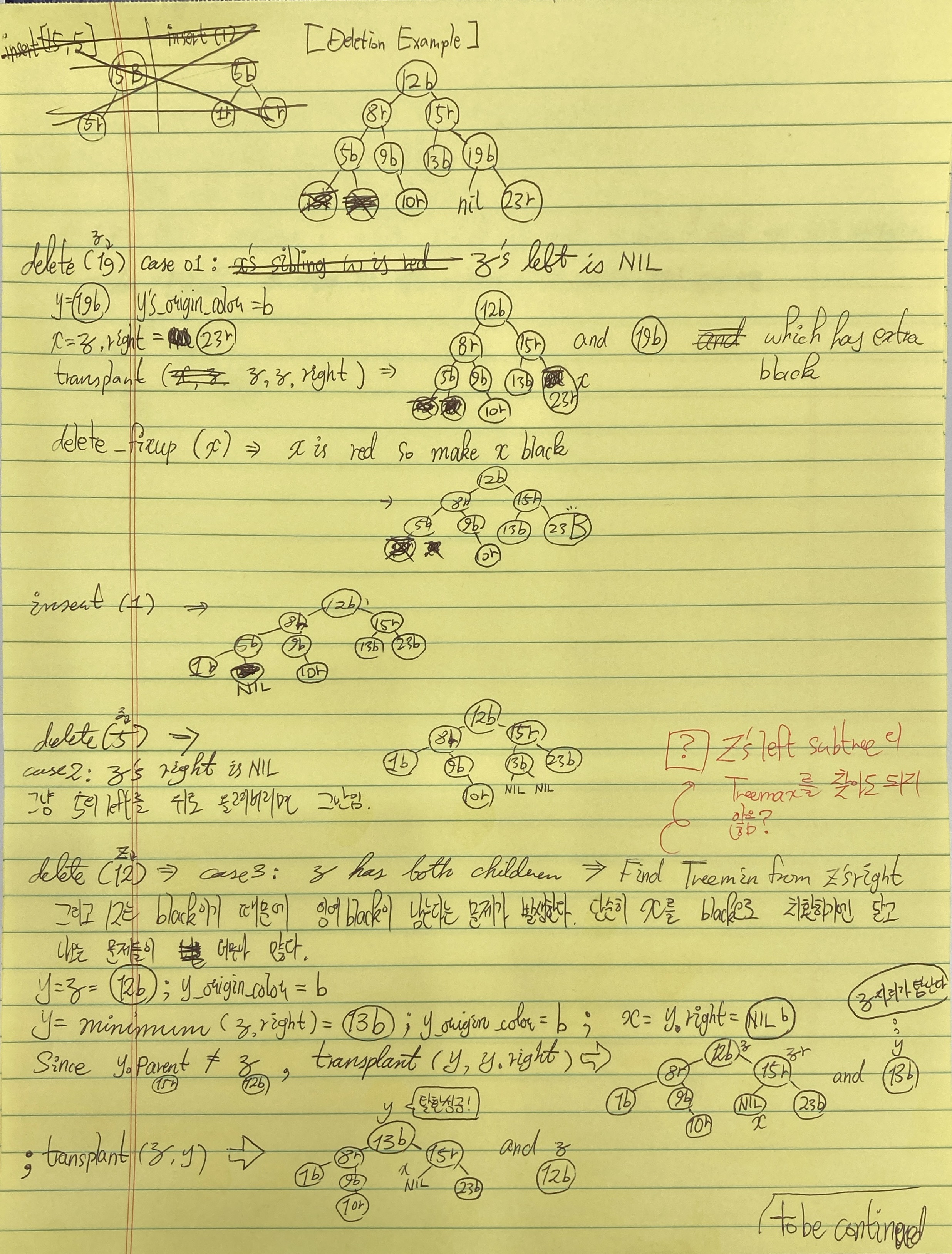
총 두 가지 스텝이 있다. 먼저 delete의 설명부터. 솔직히 case 1,2는 어렵지 않다. RBtree 제약조건을 위반하지 않으면서 단순히 NIL이 아닌 자식을 끌어올리기만 하면 그만이거든.

진짜 문제는 z의 자식이 모두 존재할 경우이다. z를 사전순으로 가장 가까운 노드인 y로 대치해야 하는데, 그 과정에서 black의 손실이 일어나기 때문이다. y를 z의 오른쪽 서브트리의 최솟값이라고 했을때, y의 왼쪽 자식은 두말할 것 없이 NIL이고, y의 오른쪽 자식을 x라고 해보자. x가 심지어 NIL일 지라도 일단 눈 한번 딱 감고 transplant를 해보자. 그러면 x는 y.p의 자식이 될 것이고 x.p는 y.p가 될 것이다. 상황에 따라서 NIL.p를 설정할 수도 있지만 괜찮다.

+) z has both children 추가: y가 직속 z의 자식이 아니라면 transplant만으로 해결하지 못한 y의 자식문제를 손봐야 한다.

transplant(tree, y, y.right)
y.right = z.right
y.right.p = y

빼버린 노드가 black 노드라면 곧 심각한 문제에 처하게 된다. black이 빠진 서브트리의 rank가 기존과 달리 1 줄어들었기 때문이다. 우리는 fixup을 수행할 때 딱 한가지만 머리에 들고 출발하면 된다.

subtree 'x'의 rank를 1 높히자. 다만 다른 서브트리가 RBTree 제약조건을 어기지 않는 선에서.

Fixup#

Example#

다음 영상의 예시를 그대로 따라가봤다. msambol 깃허브 페이지에도 파이썬 코드가 있으니 참고바란다.

FEEDBACK#

SWJungle/P7-Week04-06/pull/3 {GH} 참조

if문만 쓰다 switch 문을 보니 if와 switch 문에서 시간과 공간 복잡도에서 트레이드 오프가 있다고 들은적이 있던것 같은데 다시 공부해 봐야겠네요

if와 switch 간에 속도차이