SW Expert Academy#

Excerpt#

SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!

바쁜 일정이 지난 은기는 새로운 취미로 미술 학원을 다니기로 하였다.

마우스가 아닌 붓을 잡은 은기는, 미술 실력이 많이 부족하였다.

그래서 선생님이 그린 N×M 크기의 흑백 그림을 따라 그리며 실력을 쌓고 있다.

그러던 어느 날, 은기는 꿈을 꾸었다. 꿈에서 H×W 크기의 흑백 그림 하나를 보았다.

은기는 다음 날, 선생님의 그림 안에 꿈에서 보았던 그림이 몇 번 등장하는지 궁금하였다.

다음의 예시를 보자. 왼쪽은 은기가 꿈에서 본 그림이고, 오른쪽은 선생님이 그린 그림이다.

선생님이 그린 그림에서 은기가 꿈에서 본 그림이 등장하는 경우의 수는 다음과 같이 2가지이다.

은기가 꿈에서 본 그림과 선생님의 그림 정보가 주어질 때,

선생님의 그림에 은기가 꿈에서 본 그림이 등장하는 횟수를 계산하는 프로그램을 작성하라.

[입력]

첫 번째 줄에 테스트 케이스의 수 T가 주어진다.

각 테스트 케이스의 첫 번째 줄에는 네 개의 정수 H, W, N, M ( 1 ≤ H ≤ N ≤ 2000, 1 ≤ W ≤ M ≤ 2000 )가 공백으로 구분되어 주어진다.

다음 H개의 줄에 은기가 꿈에서 본 그림의 정보가 주어진다.

다음 N개의 줄에 선생님이 그린 그림의 정보가 주어진다.

그림은 ‘x’ 또는 ‘o’로만 이루어져 있다.

[출력]

각 테스트 케이스마다 ‘#x’(x는 테스트케이스 번호를 의미하며 1부터 시작한다)를 출력하고, 답을 한 줄에 하나씩 출력한다.

Rabin Karp 알고리즘#

참고링크

문제 난이도가 D6나 되는 덴 다 이유가 있다. 별 생각없이 풀었다가 메모리 초과 + 시간 초과로 인해 멘탈이 나가버렸다. 이차원의 큰 문자열 S를 다른 이차원의 문자열 W과 비교하여 푸는 문제로, 일차원일때엔 전에 KMP로 풀었던 것과 사실 똑같은 문제이다. 그래서 이차원일때에도 똑같이 풀어도 상관은 없었겠으나, 그래도 명색이 해시인데, 해시로 풀어보자 하고 덤벼보았다. 처음에 시도한 방법은 굉장히 단순했다.

H(W) -> key 은기가 꿈에서 본 그림 W를 일차원으로 세운 다음 해싱한 값을 key에 넣는다.
H(S[i:i+h-1][j:j+w-1]) == key 선생님의 그림의 어떤 i,j에 대하여 해싱한 값이 key와 같다면 count를 하나 늘린다. 이때 h는 W의 세로 길이, w는 W의 가로 길이이다.

위의 방식은 느렸다. i,j값에 따른 비교를 총 $N^2$ 번 하게 되는데, 해시함수 안에서 길이 h*w 짜리 문자열을 비교하고 앉아있으니 $N^3$ 시간복잡도를 가지게 된다. N,M,H,W 모두 최대 2000이므로 2000^3은 확실히 오래 걸린다.

해시를 DP처럼 풀 수는 없을까 고민하던 찰나 발견한 알고리즘이 바로 Rabin Karp 알고리즘이다. 이 알고리즘은 아래와 같은 해시함수를 사용한다. 이때 $b$는 임의의 소수로, 2 또는 31과 같은 수를 사용한다. 이 해시함수는 문자열을 부분문자열로 나누어도 $O(1)$ 시간에 그 해시값을 알아낼 수 있다는 엄청난 장점이 있다.

\[ H(W)=c_0b^0+c_1b^1+ \cdots +c_{m-1}b^{m-1} \]

표1은 H(W)의 항들을 인덱스별로 나누어 적은 표이다.

0	1	2	3	4
$c_0b^0$	$c_1b^1$	$c_2b_2$	$c_3b^3$	$c_4b^4$

[표1]

덧셈꼴로 나타내었으니 부분문자열에 대한 해시값도 구할 수 있을 것이다.

$$ \begin{flalign*}

H(W)[0:2] =& ~ c_0b^0+c_1b1+c_2b^2 \ H(W)[1:3] =& ~ c_1b^0+c_2b1+c_3b^2 \ H(W)[i:l] =& ~ c_ib^0 + c_{i+1}b^1 +\cdots + c_lb^{l - i}

\end{flalign*} $$

b의 승수에 주의하자. W의 부분 문자열도 따로 떼어놓고 보면 하나의 문자열이기 때문에 그것에 대한 해시는 반드시 $b^0$부터 시작하기 마련이다.

위의 표1에서 누적합을 구해 $\text{SUM}$ 이라는 변수에 저장했다고 치자, 그렇다면 SUM과 H(W)와의 관계는 어떻게 될까?

$$ \begin{flalign}

\text{SUM}[2] =& ~ c_0b^0+c_1b1+c_2b^2 = H(W)[0:2] \ \text{SUM}[3] - \text{SUM}[0] =& ~ c_1b^1+c_2b2+c_3b^3 = H(W)[1:3] _/ b^1 \ \text{SUM}[l] - \text{SUM}[i-1] =& ~ c_{i}b^i+c_{i+1}b+c_lb^l = H(W)[i:l] _/ b^i \

\end{flalign} $$

이차원으로 확장된 라빈 카프 알고리즘#

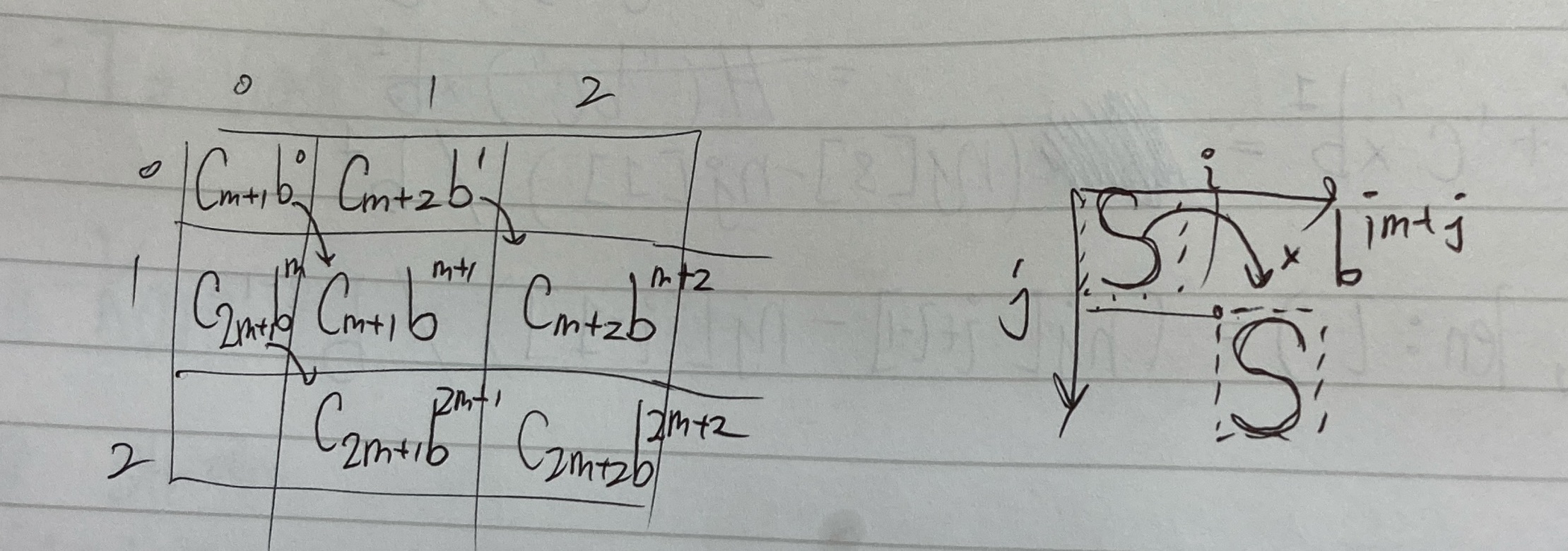
어떤 이차원 문자열 W이 다음과 같은 구성을 하고 있다고 가정하자. W는 m개의 열과 n개의 행을 갖고 있다.

c(0)	c(1)	c(2)	...
c(m)	c(m+1)	c(m+2)	...
c(2m)	c(2m+1)	c(2m+2)	...

일때 해시 누적합은 어떻게 나올까?

$c_0b^0$	$c_1b^1$	$c_2b^2$	$\cdots$
$c_mb^m$	$c_{m+1}b^{m+1}$	$c_{m+2}b^{m+2}$	$\cdots$
$c_{2m}b^{2m}$	$c_{2m+1}b^{2m+1}$	$c_{2m+2}b^{2m+2}$	$\cdots$
$\cdots$	$\cdots$	$\cdots$	$\cdots$

\[ \text{SUM}(from: [1,1], ~~to:[2,2])= c_{m+1}b^{m+1} + c_{m+2}b^{m+2} + c_{2m+1}b^{2m+1} + c_{2m+2}b^{2m+2} \]

일 것이다. 하지만 실제로 문자열 $W=\{c_{m+1},c_{m+2}, c_{2m+1}, c_{2m+2}\}$ 에 대한 해시값은

\[ \begin{align*} \text{REAL}=c_{m+1}b^0+c_{m+2}b^1 + \\ c_{2m+1}b^m+c_{2m+2}b^{m+1} \end{align*} \]

이다. 일차원때와 마찬가지로 (0,0)부터 보는 것으로 가정해야 하기 때문이다. 그러면 실제값 REAL과 SUM 간에 어떤 관계가 있을까?

\[ \text{H}(W[i:i+n-1][j:j+m-1]) \times b^{im+j} = \text{SUM}(from:[i,j], to:[i+n-1][j+m-1]) \]

\(c_0b^0\)	\(c_1b^1\)	\(c_2b^2\)	\(\cdots\)
\(c_mb^m\)	\(c_{m+1}b^{m+1}\)	\(c_{m+2}b^{m+2}\)	\(\cdots\)
\(c_{2m}b^{2m}\)	\(c_{2m+1}b^{2m+1}\)	\(c_{2m+2}b^{2m+2}\)	\(\cdots\)
\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)