Skip to content

상태: 풀이완료
태그: graph, tree

영준이의 진짜 BFS - swea

개요#

트리 자료구조에서 임의의 두 노드의 가장 가까운 조상을 찾는 문제가 있다. 예를 들어 트리 구조가 다음과 같다고 가정해보자

 0
 ├─ 1
 │  ├─ 5
 │  └─ 9
 ├─ 2
 │  ├─ 3
 │  │  └─6
 │  ├─ 4
 │  └─ 8
 │     └─10
 └─ 7

1과 2의 공통조상은 0이다. 5와 9의 공통조상은 1이다. 9와 3의 공통조상은? 0이다.

Naive 코드#

LCA 몰랐을 때 O(N)으로 푼 나의 코드. ancester() 는 노드의 부모들을 줄줄이 모아만든 벡터를 리턴한다. 맨 뒤에서부터 하나씩 비교해가며 동일한 조상이 아닐때까지 반복한다.

9의 조상은 {0, 1}, 10의 조상은 {0, 2, 8} 이다. 따라서 앞에서부터 따라 읽어가다 마지막으로 조상이 일치하는 케이스만 리턴하면 된다.

inline auto nearest_common_ancester(node_t const *n1, node_t const *n2)
    -> node_t const & {
  vector<node_t *> ancester1 = ancester(*n1);
  vector<node_t *> ancester2 = ancester(*n2);

  const auto size1 = ancester1.size();
  const auto size2 = ancester2.size();
  auto len = std::min(size1, size2);

  node_t *ret = ancester1[size1 - 1];

  for (size_t i = 1; i <= len; ++i) {
    if (ancester1[size1 - i]->id != ancester2[size2 - i]->id) {
      return *ancester1[size1 - (i - 1)];
    }
    ret = ancester1[size1 - i];
  }

  return *ret;
}

LCA - Lowest Common Ancestor#

https://www.youtube.com/watch?v=dOAxrhAUIhA

LCA 알고리즘에도 여러 종류가 있지만 저 유튜브 영상을 참고하여 Binary Lifting과 파라메트릭 서치를 활용하여 \(O(\sqrt{N})\) 시간과 \(O(N\sqrt{N})\) 공간을 사용한 알고리즘을 하나 알게 되었다.

Binary Lifting#

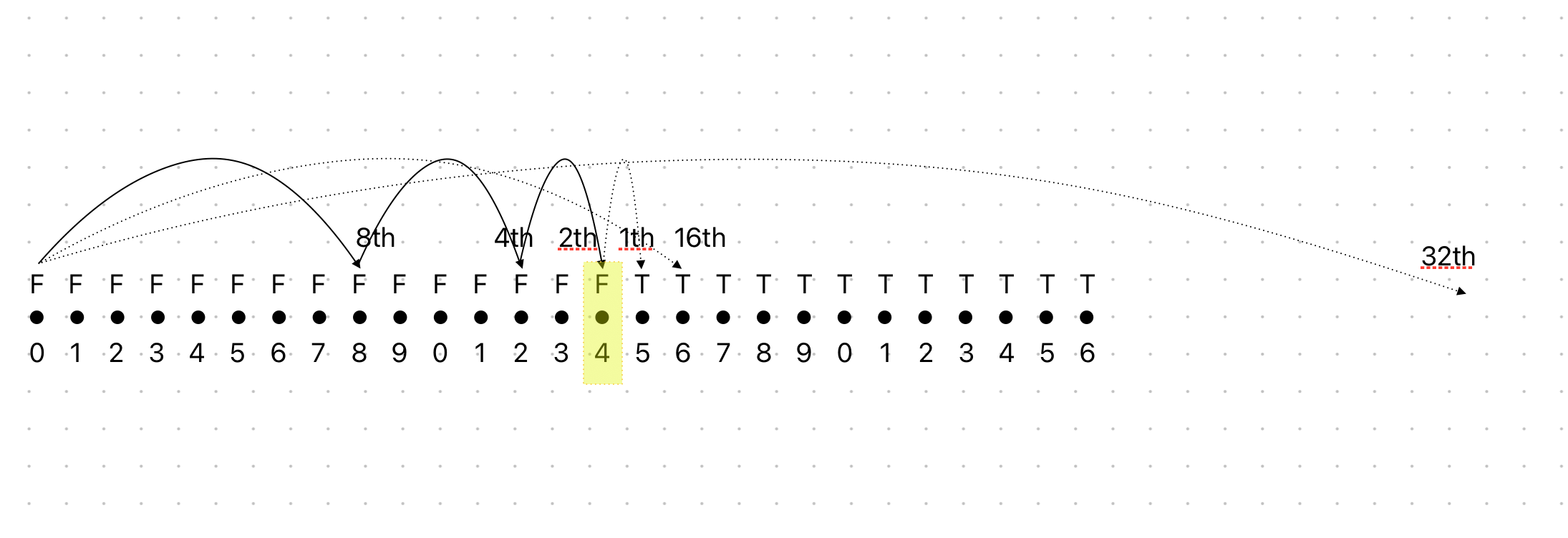
빠르게 k-th ancestor를 찾기 위해 우리는 모든 노드에 대한 조상 리스트를 저장하는 방법을 고안할 수 있다. 이러면 k-th ancestor를 찾는데 단 O(1)의 시간복잡도면 가능하다. 하지만 공간낭비가 심하다. 모든 정점들에 대하여 만들어야 하기 때문에 O(\(N^2\)) 공간복잡도가 필요하다. 이는 좋지 못한 현상이다. 따라서 아주 신박하게 k-th 가 아니라 \(2^k\)-th ancester만을 저장하는 방법을 고안했다.

아래의 코드는 up 배열을 만들기 위한 전처리 작업을 표현했다.

int up[N][LOG] = {0}; // up[v][j] = 2^j-th ancestor of v

void init() {
  for (v = 0..<N) {
    up[v][0] = parent[v]; // 2^0 == 1이니까 
    /**
      up[v][1] = up[ up[v][0] ][0] --> 2-th ancestor = 1-th ancestor의 1-th ancestor
      up[v][2] = up[ up[v][1] ][1] --> 4-th ancestor = 2-th ancestor의 2-th ancestor
        ...
        */
        for (j = 1..<LOG) {
            up[v][j] = up[ up[v][j-1] ][j-1]
        }
  }
}

LCA-brute force#

위의 영상에서는 일단 한 칸씩 올라가는 코드를 먼저 작성했다. A, B 중 A가 더 낮은 depth를 가지고 있다고 했을 때 B의 depth와 동일할때까지 parent를 타고 올라온다. 그리고 A == B일때까지 서로 한 칸씩 올라가고 A를 리턴해버리면 된다. 

int get_lca(int a, int b) {
    if (depth[a] < depth[b]) {
        swap(a, b);
    }
    while (depth[a] > depth[b]) {
        a = parent[a];
    }
    while (a != b) {
        a = parent[a];
        b = parent[b];
    }
    return a;
}

LCA -with-binary-lifting#

이제 진짜 lowest common ancestor를 찾아보자. 여기에서 기존처럼 하나씩 올라가면 의미가 없다. 따라서 파라메트릭 서치를 통해 한 번에 성큼성큼 lca와의 거리를 좁혀보자.

Parametric Search

a, b의 depth를 맞춰주기 위해 k 변수를 활용하는데, k가 굳이 2의 제곱수가 아니어도 된다는 것을 이용한 영리한 예이다. 예를 들어 거리가 12(0b1100)라면, 단지 12 = 4 + 8 이므로 j = 2, j = 3일때에만 움직이면 된다.

코드에서 알 수 있는 건, lca 이후의 조상들은 굳이 가지 않는다는 것이다. 따라서 lca 직전 노드까지 이동하는 것을 목표로 삼을 수 있다. j가 하나씩 줄어드는거랑 lca 직전노드랑 무슨 상관이지 싶을 수 있는데, 직접 그림을 그려보면 공통조상이 아닐때에만 성큼성큼 이동하다보면 결국 lca 직전에 도달함을 알 수 있다.

int lca(a, b) {
  if (depth[a] < depth[b]) {
    swap(a, b);
  }
  // a와 b의 depth를 맞춰준다.
  int k = depth[a] - depth[b]; 
  for (int j = LOG-1...0) {
    if (k & (1 << j)) { // k의 j번째 비트가 켜져있으면
            a = up[a][j];
    }
  }
  if (a == b) { // 알고보니 b가 a의 조상이었던 거임~
    return a;
  }
  for (int j = LOG-1...0) {
        if (up[a][j] != up[b][j]) { // 공통조상이 아니라면
            a = up[a][j];
            b = up[b][j];
        }
    }
    return up[a][0]; // lca 바로 직전 노드에서 멈췄으니 한 칸 올라가줘야지
}

lca.png

관련 문제#